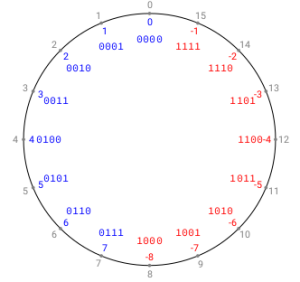
Représentation des entiers relatifs
Première tentative
Contexte et hypothèse
On se place dans le cas où on a 4 bits pour coder les nombres. On peut donc coder 16 nombres entiers.
On souhaite maintenant avec ces 4 bits coder des nombres entiers relatifs. On peut toujours coder 16 entiers mais 7 négatifs, 8 positifs et le zéro ou 8 négatifs, 7 positifs et le zéro.
Pour coder le signe positif ou nul, on propose naturellement de le coder sur un bit : 0 pour positif et 1 pour négatif.
On obtient alors les 15 entiers naturels suivants codés sur 4 bits :
1111 ; 1110 ; 1101 ; 1100 ; 1011 ; 1010 ; 1001 ; 0000 ; 0001 ; 0010 ; 0011 ; 0100 ; 0101 ; 0110 ; 0111
Il reste le code binaire 1000 qui selon la convention est le négatif de zéro.
Attention : Problèmes
Le premier c'est le double encodage du zéro en 0000 et 1000
Ensuite l'addition de ces nombres pose un pb :
0101 + 1110 = 11011 soit 1011 sur 4 bits c'est à dire que 5 + (-6) = -3
0101 + 1011 = 10000 soit 000 sur 4 bits c'est à dire que 5 + (-3) = 0
Définition : Opposé d'un nombre
L'opposé d'un nombre a est le nombre noté -a tel que a + (-a) = 0, c'est à que c'est le nombre qui répond à l'équation a + x = 0.
Construire les opposés.
Méthode : addition modulaire.
On se place dans le cas où on a 4 bits pour coder les nombres. On peut donc coder 16 nombres entiers.
On prends les 7 premiers nombres entiers positifs codés : 0001 ; 0010 ; 0011 ; 0100 ; 0101 ; 0110 ; 0111
Il reste donc les 8 autres codages binaires pour trouver opposés.
Au lieu de définir -5 à partir de la notation, c'est à dire de prendre le codage de 5 et de changer le bit de poids fort de zéro à 1, on construit - 5 à partir de la définition de l'opposé d'un nombre.
(Rappelons qu'avec un codage en 4 bits, 10000 = 0000.)
On chercher donc le nombre binaire tel que 0101 + xxxx = 0000. On trouve 1011 car 0101 + 1011 = 10000 soit 0000 sur 4 bits. Donc le nombre -5 est codé en binaire 1011.
Définition : Les entiers relatifs sur 4 bits.
Sont construits avec la méthodes précédentes les codes binaires des 16 entiers relatifs.
Remarque :
Cette méthode construit des entiers relatifs qui respecte l'arithmétique \(x+y \equiv 0\) modulo \(2 ^4\)
On retrouve le bit de poids fort pour coder le signe du nombre
Complément à deux
Complément : Description de la méthode de complément à 2
Inverser tous les bits (complément à 1)
ajouter 1 au nombre binaire obtenu
On obtient l'écriture binaire de l'opposé du nombre.
Exemple : Trouver sur un octet l'écriture des nombres en base 10
-10 ; -128 ; -42 ; 97
Solutions :
\((-10)_{10} = (1111 0110)_2\)
\((-128)_{10} = (1000 0000)_2\)
\((-42)_{10} = (1101 0110)_2\)
\((97)_{10} = (0110 0001)_2\)
Exemple : Donner en base 10 la valeur des octets signés
1110 0111
1100 0001
\((1110 0111)_2=( -25)_{10}\)
\((1100 0001)_2 = (-63)_{10}\)
Complément : Coder le complément à un et à deux d'une chaîne de caractère en binaire.
Ecrire deux fonctions, respectivement le complément à un, cp1() et le complément à deux, cp2() qui prennent en paramètre une chaîne de caractère d'un code binaire et qui renvoient respectivement la chaîne de caractère du complément à 1, du complément à deux.