Représentation des données : les nombres entiers naturels
Objectifs
Écriture d'un entier dans une base supérieure à deux
Passer d'une représentation d'un nombre d'une base dans une autre.
pré-requis
Divisions Euclidiennes
Base décimale
Notion de base : la numération décimale (10)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Dans le système décimal, on utilise 10 chiffres de 0 à 9. Le système décimal est donc un système de numération de base 10. Ainsi les nombres se décomposent en une somme de facteurs de \(10^n\)
Exemple :
Le nombre 4138 peut s'écrire : 4 × 1000 + 1 × 100 + 3 × 10 + 8 × 1
En partant de la droite :
Le 1er chiffre (de rang 0) correspond aux unités : \(10^0 = 1\)
Le 2ème chiffre (de rang 1) correspond aux dizaines :\(10^1 =10\).
Le 3ème chiffre (de rang 2) correspond aux centaines \(10^2 =100\).
La position (ou rang) de chaque chiffre dans le nombre est importante , elle définit le poids du chiffre
dans le nombre :
Le chiffre de poids le plus fort correspond à celui dont la puissance de 10 est la plus grande (coté gauche). C'est ce chiffre qui indique l'ordre de grandeur du nombre
Le chiffre de poids le plus faible correspond à celui dont la puissance de 10 est la plus petite (côté droit)
\(10^3\) | \(10^2\) | \(10^1\) | \(10^0\) |
4 | 1 | 3 | 8 |
Chiffre de poids le + fort | Chiffre de poids le + faible |
Exemple :
décomposer \((265301)_{10}\)
Besoin de l'informatique
Un ordinateur fonctionne grâce à l'usage de transistors.
(mettre une illustration, et éventuellement une capture d'un oscilloscope)
Un transistor ne connaît que deux états :
un état électrique dit "bas" qui correspond souvent à une tension électrique proche de zéro volt,
l'état électrique "haut" correspond à quelques volts.
Nous pouvons également dire 0 pour faux (quand le courant ne passe pas) et 1 pour vrai (quand le courant passe).
Ce codage est nommé base binaire et est utilisé par l'ordinateur pour comprendre et traiter les données.
Un 0 ou un 1 constitue ce que l'on appelle un bit (binary digit). Dans le processeur (qui traite les données) ou dans la RAM ( Random Access Memory), qui stocke l'information, les bits sont regroupés par paquet de huit. Ce groupe de huit bits est appelé un octet.
Les humains quant à eux travaillent avec dix chiffres, c'est la notation décimale (base 10).
L'hexadécimal (base 16) est également utilisé dans le monde informatique. C'est en effet assez courant de regrouper plusieurs bits (un bit correspond à un "1" ou à un "0") et de les transformer en hexadécimal. Cette transformation permet de faciliter la tache des programmes et des programmeurs.
Par exemple la valeur en binaire \((0011 1010)_2\) est assez dure à mémoriser de tête pour un humain, il est donc judicieux d'utiliser l'hexadécimal pour désigner cette même valeur : \((0011 1010)_2\) est égal en hexadécimal à \((3A)_{16}\) . L'hexadécimal permet une écriture plus condensée du binaire.
Remarque : Les nombres entiers en Python
En python, les nombres entiers peuvent être de taille arbitraire (ce qui n'est pas le cas dans de nombreux langages de programmation). Les entiers ne sont limités que par la taille de la mémoire disponible pour les stocker.
Le codage binaire
Dans le système binaire, on utilise 2 symboles les chiffres : 0 et 1.
Le système binaire est donc un système de numération de base 2. Ainsi les nombres binaires se décomposent (en décimal) en une somme de facteurs de \(2^n\).
Exemple :
Le nombre binaire \((100111)_2\) correspond (en décimal) à
\((1 × 2^5 + 0 × 2^4 + 0 × 2^3 + 1 × 2^2 + 1 × 2^1 + 1 × 2^0 )_{10}\)
\((1 × 32 + 0 × 16 + 0 × 8 + 1 × 4 + 1 × 2 + 1 × 2)_{10}\)
\(( 32 + 0 + 0 + 4 + 2 + 1 ) 10 = (39)_{10}\)
En partant de la droite :
Le 1er bit (de rang 0) correspond aux unités : \(2^0 =1\)
Le 2ème bit (de rang 1) correspond aux deuzaines : \(2^1 =2\)
Le 3ème bit (de rang 2) correspond aux quatraines : \(2^2 =4\)
............
La position (ou rang) de chaque bit dans le nombre est importante , elle définit le "poids" du bit dans le nombre :
Le bit de poids le plus fort correspond à celui dont la puissance de 2 est la plus grande (coté gauche)
Le bit de poids le plus faible correspond à celui dont la puissance de 2 est la plus petite (côté droit)
\(2^5\) | \(2^4\) | \(2^3\) | \(2^2\) | \(2^1\) | \(2^0\) |
1 | 0 | 0 | 1 | 1 | 1 |
chiffre de poids le plus fort | chiffre de poids le plus faible |
Remarque : Représentation des entiers en Python
Par défaut en Python, les nombres entiers saisis ou affichés sont en base 10 et illimités. Pour manipuler des séquences de bits, de longueur arbitraire, on utilise la notation 0b... où il suffit de remplacer les ... par des 0 et des 1.
Remarque :
Les nombres pairs finissent par 0 et les impairs par 1
Méthode : D'une base binaire à décimale
Méthode générale :
\((xyzw)_2 = ( x × 2^3 + y × 2^2 + z × 2^1 + w × 2^0 )_{10} = (....)_{10}\)
Exemple : Applications : Convertir le nombre suivant en base décimale
Donner la valeur décimale de \((10100110)_2\)
\((1101 0100 0101 1011)_2\)
combien de nombre entier peut-on coder avec un octet (8 bit)? 2 octets ?
Méthode : Compter sur ces doigts en binaire
Retrouver sur ses mains le comptage en binaire.
Remarque : on utilise la base dix car nous avons 10 doigts ?
Méthode : Un algorithme
Ecrire un algorithme sur papier qui permet à quelqu'un qui exécute vos instructions de déterminer la valeur décimale d'un nombre binaire donné.
Méthode : Autre principe algorithmique
A partir du nombre suivant \((11001100)_2\), on peut retrouver l'écriture décimale en lisant les chiffres de gauche à droite (sens naturel de lecture) .
On part de la valeur 0 et à chaque étape on multiplie le résultat de l'étape précédente par 2 et on ajoute le chiffre lu. On arrête quand on n'a plus de chiffre à lire.
Retrouver l'écriture décimale du nombre ci-dessus en appliquant la méthode.
Explication :
\(1 \times 2^0\)
\(1 \times 2^1 +1\times 2^0\)
\(1 \times 2^2 + 1 \times 2^1 +0 \times 2^0\)
\(1 \times 2^3 + 1 \times 2^2 +0 \times 2^1 + 0 \times 2^0\)
\(1 \times 2^4 + 1 \times 2^3 +0 \times 2^2 + 0 \times 2^1 + 1\times 2^0\)
\(1 \times 2^5+ 1 \times 2^4 +0 \times 2^3 + 0 \times 2^2 + 1\times 2^1+ 1 \times 2^0\)
\(1 \times 2^6+ 1 \times 2^5 +0 \times 2^4 + 0 \times 2^3 + 1\times 2^2+ 1 \times 2^1 + 0 \times 2^0\)
\(1 \times 2^7+ 1 \times 2^6 +0 \times 2^5 + 0 \times 2^4+ 1\times 2^3+ 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0\)
Remarque :
Ce principe fonctionne aussi pour la base décimale :
2507 :
\(2 \times 10^0\)
\(2 \times 10^1 +5 \times 10^0\)
\(2 \times 10^2 + 5 \times 10^1 + 0 \times 10^0\)
\(2 \times 10^3 + 5 \times 10^2 +0 \times 10^1 + 7 \times 10^0\)
Addition et multiplication sur les nombres entiers naturels
Méthode :
a | b | a+b | \(a \times b\) |
|---|---|---|---|
0 | 0 | ||
0 | 1 | ||
1 | 0 | ||
1 | 1 |
Simulation : Pour poursuivre la découverte
Méthode :
Effectuer en posant l'opération les calculs suivants en binaire :
101+11 ; 1101+ 11001 ; \(101 \times 11\)
Calculer la somme binaire suivante de deux manières : 1010+1010+1010+1010
Convertir l'écriture d'un nombre décimal en binaire
Exemple :
Comment convertir en binaire le nombre 2712892 ?
Méthode : Convertir de décimale à binaire
Convertir \((42)_{10}\) en base deux
On applique la méthode de division par 2 :
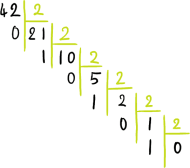
\(42=2 \times 21+ 0\)
\(42=2 \times (2 \times 10 +1) + 0\)
\(42=2 \times (2 \times (2 \times 5 +0)+1) + 0\)
\(42=2 \times (2 \times (2 \times (2 \times 2+1)+0) +1) + 0\)
\(42=2 \times (2 \times (2 \times (2 \times (2 \times 1 +0 )+1) +0)+1) + 0\)
\(42=2 \times (2 \times (2 \times (2 \times (2 \times (2 \times 0 +1) +0 )+1) +0)+1) + 0\)
Donc :
\(42 = 1 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0\)
d'où \((42)_{10} = (101010)_2\)
Exemple : Application
Convertir en base 2 les nombres suivants exprimés dans la base 10 :
a) 24 c) 128 e) 1024
b) 19 d) 789 f) 1245
\((24)_{10}=(11000)_2\) ;
\((19)_{10}=(10011)_2\) ;
\((128)_{10}=(10000000)_2\) ;
\((789)_{10}=(1100010101)_2\) ;
\((1024)_{10}=(10000000000)_2\) ;
\((1245)_{10}=(10011011101)_2\) ;
Le codage Hexadécimal
On utilise 16 signes distincts pour le codage ; Le système hexadécimal est un système de numération de base 16.
L'hexadécimal utilise les 10 chiffres habituels auxquels on ajoute les 6 premières lettres de l'alphabet en majuscules : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (pour 10) , B (pour 11), C (pour 12), D(pour 13), E (pour 14), F (pour 15).
Ainsi les nombres hexadécimaux se décomposent (en décimal) en une somme de facteurs de \(16^n\)
Exemple :
Le nombre hexadécimal \((FAC)_{16}\) correspond en décimal à :
\(( F×16^2 + A×16^1 + C×16^0 )_{10}\)
\(( 15×256 + 10×16 + 12×1 )_{10}\)
\(( 3840 + 160+ 12)_{10} =(4012)_{10}\)
En partant de la droite :
Le 1 er chiffre (de rang 0) correspond aux unités : \(16^0 =1\)
Le 2ème chiffre (de rang 1) correspond aux "seizaines" : \(16^1 =16\)
Le 3ème chiffre (de rang 2) correspond aux "deux-cent-cinquante-sizaines" : \(16^2 =256\)
............
La position (ou rang) de chaque chiffre dans le nombre est importante , elle définit le "poids" du chiffre dans le nombre :
Le chiffre (lettre) de poids le plus fort correspond à celui dont la puissance de 16 est la plus grande (gauche)
Le chiffre (lettre) de poids le plus faible correspond à celui dont la puissance de 16 est la plus petite (droite)
\(16^5\)
\(16^4\)
\(16^3\)
\(16^2\)
\(16^1\)
\(16^0\)
8
2
D
A
B
7
bit de poids le plus fort
bit de poids le plus faible
Rappel :
Décimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Binaire | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Hexadécimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Méthode : D'une base hexadécimale à décimale
\((xyzw)_{16} = ( x × 16^3 + y × 16^2 + z × 16^1 + w × 16^0 )_{10} = (....)_{10}\)
Convertir l'écriture d'un nombre d'une base à l'autre.
Remarque : En Python
De la même manière on peut manipuler des nombres hexadécimaux à l'aide de la notation 0x...où...désigne n'importe quelle séquence de chiffre en base 16.
Exemple : Exercice d'application
Convertir en base dix les nombres suivants exprimés dans différentes bases :
a) \((14)_{16}\) ; b) \((ABC)_{16}\) ; c) \((35ED12F )_{16}\)
Vérifier les réponses avec Python en utilisant la notation 0x14 pour le nombre hexadécimal.
réponses : a) 20 b)2748 c)56545583
Méthode : Convertir de décimal en hexadécimal
Méthode par division : on effectue une succession de divisions par 16, comme pour le binaire, puis on range l 'ensemble des
restes : ( celui de la première division étant celui de poids le plus faible ) pour constituer le code dans la nouvelle base .
Exemple, convertir 194 en base 16 :
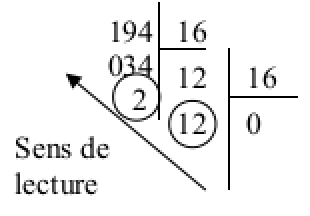
Résultat :
\(194=16 \times 12 +2\) soit \(12 \times 16^1 + 2 \times 16^0\)
donc,
12 et 2 soit \((C2)_{16}\)
Exemple : Application
Convertir en base 16 les nombres suivants exprimés dans la base 10 :
a) 24 c) 128 e) 1024
b) 19 d) 789 f) 1245
\((24)_{10}=(18)_{16}\)
\((19)_{10}=(13)_{16}\)
\((128)_{10}=(80)_{16}\)
\((789)_{10}=(315)_{16}\)
\((1024)_{10}=(400)_{16}\)
\((1245)_{10}=(4dd)_{16}\)
Remarque : Convertir en hexadécimal en passant par l'écriture binaire
On commence par coder le nombre en binaire , puis on regroupe à partir de la droite par tranche de quatre bits puis on code chaque regroupement dans la base hexadécimale.
Méthode : Convertir de binaire à hexadécimal
Il faut décomposer le nombre binaire en quartets (donc des blocs de 4 bits consécutifs 4 par 4).
Pour l'octet \((01111101)_2\) on le sépare 2 quartets : 0111 – 1101. Chaque quartet binaire représente un nombre décimal : 7 – 13 ce qui donne \((7D)_{16 }\).
Méthode : Convertir un hexadécimal en binaire
Convertir \((82DAB7)_{16}\) . on prend chaque chiffre de l'écriture hexadécimale et on l'écrit en base deux.
Soit 8-2-13-10-11-7 c'est à dire 1000-0010-1101-1010-1011-0111 donc en binaire \((1000 0010 1101 1010 1011 0111)_2\)
Exemple : Application : Reprendre l'exemple précédent
\((24)_{10}=(11000)_2\) ; \((24)_{10}=(18)_{16}\)
\((19)_{10}=(10011)_2\) ; \((19)_{10}=(13)_{16}\)
\((128)_{10}=(10000000)_2\) ; \((128)_{10}=(80)_{16}\)
\((789)_{10}=(1100010101)_2\) ; \((789)_{10}=(315)_{16}\)
\((1024)_{10}=(10000000000)_2\) ; \((1024)_{10}=(400)_{16}\)
\((1245)_{10}=(10011011101)_2\) ; \((1245)_{10}=(4dd)_{16}\)
Exemple : Le codage des images
On reconstitue les couleurs en informatique à partir du rouge, du vert et du bleu. Sachant que chaque couleur est codée par un octet, combien de couleurs peut-on ainsi reconstituer?
Remarque: le blanc est codé par: FF FF FF; le noir est codé par 00 00 00. (chaque groupe de deux chiffres code une couleur, dans l'ordre: rouge, vert, bleu).
La couleur vert d'eau sur le moniteur est codée en hexadécimal \((82DAB7)_{16}\) .