Repérage sur la Terre
Fondamental : Coordonnées géographiques
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Définition :
Grand cercle : intersection de la terre avec un plan passant par le centre de la terre.
Petit cercle : intersection de la terre avec un plan quelconque ne passant pas par le centre de la terre.
Equateur : grand cercle perpendiculaire à l’axe des pôles, séparant hémisphères sud et nord
Parallèle : petit cercle parallèle à l’équateur
Méridien : demi-grand cercle passant par les 2 pôles. Par convention, le méridien d’origine (0°) est celui qui passe par l’observatoire astronomique de la ville de Greenwich (Angleterre).
Définition : Coordonnées géographiques
Latitude : Angle compris, à partir du centre de la terre, entre l’équateur et le parallèle du point considéré.
La latitude est NORD si le point considéré est situé dans l’hémisphère nord.
La latitude est SUD si le point considéré est situé dans l’hémisphère sud.
Au pôle, latitude = 90°
A l’équateur, latitude = 0°
0° ≤ latitude ≤ 90°
Longitude : Angle compris, à partir du centre de la terre, entre le méridien de Greenwich et le méridien du point considéré.
La longitude est OUEST ou négative si le point considéré est à l’ouest du méridien de Greenwich.
La longitude est EST ou positive si le point considéré est à l’est du méridien de Greenwich.
Au méridien de Greenwich, longitude = 0°
0° ≤ longitude ≤ 180°
Définition : Loxodromie, orthodromie
Une loxodromie , est une courbe qui coupe les méridiens d'une sphère sous un angle constant. C'est la trajectoire suivie par un navire qui suit un cap constant.
L'orthodromie désigne le chemin le plus court entre deux points d'une surface. Sur une sphère, c'est le plus petit des deux arcs du grand cercle joignant les deux points.
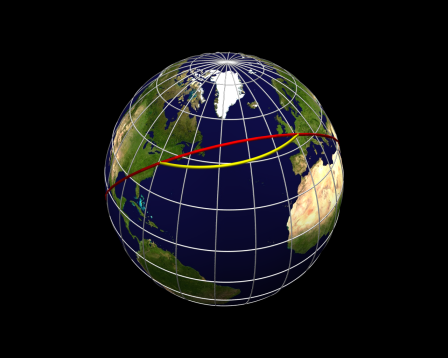
Pour en savoir plus :
Définition : Mesures de distances
Distances horizontales : le Mile Nautique (NM)
Longueur d’une minute d’angle de grand cercle
Rappel : 1°=60 minutes d’angle
1 NM = 1,85 km
Distances verticales : le Pied (ft)
Pour transformer les mètres en pieds, on multiplie par 10/3.
Pour transformer les pieds en mètres, on multiplie par 3/10.
1 ft = 0,30 m