Algorithmes gloutons
Définition :
Les algorithmes gloutons font partie des algorithmes d'optimisation dont l'objectif est de trouver une « bonne » solution selon un certain critère mais cela ne sera pas forcément la meilleure solution possible.
Un algorithme glouton va faire un choix selon un critère à un moment donné. Ce choix sera optimal parmi un ensemble de choix restreint. Il sera « localement » optimal. Pour résoudre un problème, l'algorithme glouton va donc faire des choix locaux qui on l'espère finira à aboutir à une solution globale optimale. Ce sera parfois le cas mais pas toujours. Mais on obtiendra une « bonne » solution, alors que nous nous n'en n'obtenons pas toujours de bonnes en faisant une étude exhaustive de toutes les possibilités en vue de choisir la meilleure (cf. l'exemple du voyageur de commerce).
Fondamental : Algorithme glouton pour le rendu de monnaie
La monnaie euros forme ce que l'on appelle un système canonique, c'est-à-dire un système pour lequel l'algorithme glouton donne toujours un rendu optimal.
Un système non canonique est par exemple celui-ci où l'algorithme Glouton ne va pas trouver la solution optimale alors qu'elle existe. C'était le cas de l'ancienne monnaie anglaise avant la réforme de 1971 : La livre était divisée en 20 shillings et un shilling valait 12 pence.
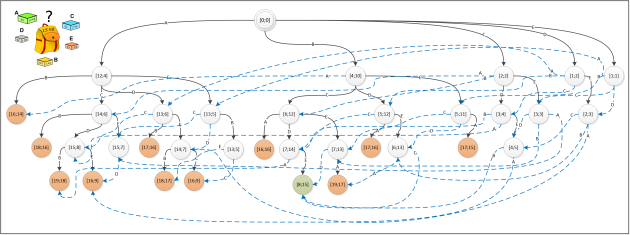
Méthode : Le problème du sac à dos
Ce genre de problème est un grand classique en informatique, on parle de problème d'optimisation. Il existe toujours plusieurs solutions possibles à un problème d'optimisation mais on ne cherche pas n'importe quelle solution, on cherche une solution dite optimale : dans le problème du sac à dos, on cherche le plus grand gain possible. Souvent, dans les problèmes d'optimisation, il n'existe pas une solution optimale, mais plusieurs solutions optimales, résoudre un problème d'optimisation c'est donc trouver une des solutions optimales.
Attention :
En apparence, la solution la plus simple dans le cas du sac à dos serait d'écrire un algorithme qui teste toutes les combinaisons d'objets possibles et qui retient les solutions qui offrent un gain maximum.
Dans le cas du problème du sac à dos, avec seulement 5 objets, cette solution pourrait être envisagée, nous obtenons le graphe suivant :
Mais avec un plus grand nombre d'objets, on retombe dans le même configuration qu'avec le problème du voyageur de commerce, le temps de calcul, même pour un ordinateur très puissant, deviendrait trop important.
En effet, l'algorithme qui testerait toutes les combinaisons possibles aurait une complexité en temps en O(\(a^n\)) avec a une constante et n les nombre d'objets. On parle d'une complexité exponentielle. Les algorithmes à complexité exponentielle ne sont pas efficaces pour résoudre des problèmes, le temps de calcul devient beaucoup trop important quand n devient très grand.
À la place de cette méthode "je teste toutes les possibilités", il est possible d'utiliser un algorithme glouton.
Fondamental : L'algorithme glouton n'est pas optimal.
La solution trouvée ci-dessus est-elle optimale ?
Il est important de bien comprendre qu'un algorithme glouton ne donne pas forcement une solution optimale. Pour certains types de problèmes, il est possible de démontrer qu'un algorithme glouton donnera toujours une solution optimale, mais cela dépasse largement le cadre de ce cours.